|
sjm213
有小知識,無大學問。
級別: 論壇版主

   |
一、數制與碼制 1- 基本概念 不同的數碼可以用來表示數量的不同大小。用數碼表示數量大小時,僅用一位數碼往往不夠用,因此經常需要用進位計數制的方法組成多位數碼使用。 把多位數碼中每一位的構成方法以及從低位到高位的進位規則稱為數制。在數字電路中經常使用的計數進制有十進制、二進制和十六進制。有時也用到八進制。 不同的數碼不僅可以用來表示數量的不同大小,而且可以用來表示不同的事物或事物的不同狀態。在用于表示不同事物的情況下,這些數碼已經不再具有表示數量大小的含義了,它們只是不同事物的代號而已。這些數碼稱為代碼。 為了便于記憶和查找,在編制代碼時總要遵循一定的規則,這些規則就稱為碼制。 2- 幾種常用的數制  4. 十六進制數(Hexadecimal) 十六進制數的進位規則是“逢十六進一” ,其進位基數R=16,采用的16個數碼為0、 1、 2、…、 9、A、 B、 C、 D、 E、 F。 符號A~F分別代表十進制數的10~15。每位的權是16的冪。 任何一個十六進制數, 可以表示為:  5. 不同進制數的對照表 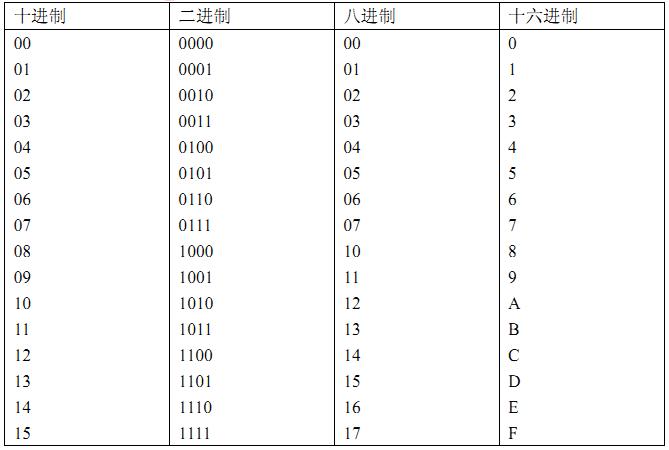 |
|---|---|
|
|
|
feng-xing
級別: 略有小成

|
學習了,下面例題中好像少了乘號。3- 不同數制之間的轉換 1. 其它進制轉換為十進制 方法是:將其它進制按權位展開,然后各項相加,就得到相應的十進制數。 例1: N=(10110.101)B=(?)D 按權展開N=1*24+0*23+1*22+1*21+0*20+1*2-1+0*2-2+1*2-3 =16+4+2+0.5+0.125 =(22.625)D 例2: N=(532.8)H=(?)D 按權展開N=5*162+3*161+2*160+8*16-1 =1280+48+2+0.5 =(1330.5)D |
|---|---|
|
|






 滬公網安備31010802001143號
滬公網安備31010802001143號